问题背景

AC自动机是一个解决多模式匹配的问题的典型模型，特别是应用于字符串匹配问题。多模式匹配简单来说就是如下的问题：

多模式匹配问题

给定一个字符串数组words和一个文本内容s，找到s中出现的所有属于words中的字符串。

许多编程语言中常用的substr函数（从一个字符串中找到某个子字符串）就是这个问题的一种特殊情况（即words中仅有一种匹配模式）。

字典树

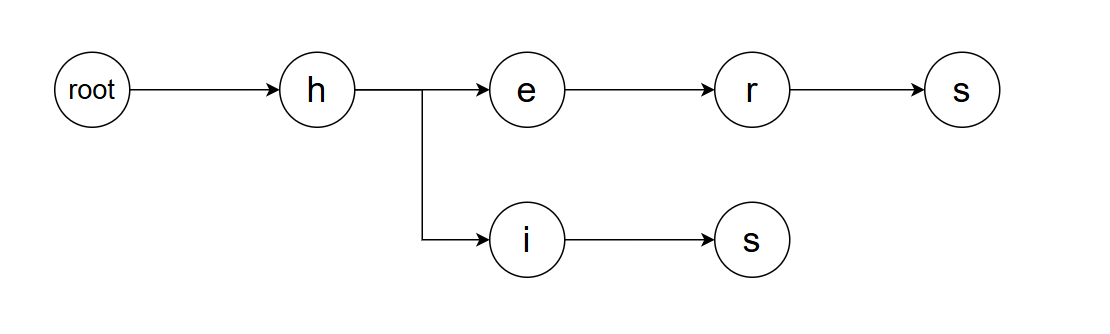
在多模式匹配中，我们如何存储这些模式是首先需要解决的问题：如果使用最简单的存储方法，即将每一个模式都完全存储，那么其占用的空间将会是words中所有单词长度的总和。 在大数量的任务下，这个数字会很恐怖！ 利用树的数据结构，很容易构造出一个较为节省空间的存储方案： 将具有相同前缀的模式的重复部分合并，构造成树的形状。 例如，我们要存储单词hers和his时，就可以如下组织这棵树。我们一般称这棵树为 字典树 。

字典树
字典树

显然，在模式数量很大的情况下，这种存储方案能够为我们节省大量的存储空间。构建这棵树的方法也很简单，我们仅需遍历所有模式，在每个模式开始时，从根节点向后查找：如果已有我们需要的子节点，则直接转移至子结点上；否则，创建之。构建字典树所需要的时间复杂度为O(w×l)O(w\times l)，其中：ww是模式长度（彼此可能不一），ll是模式数。

字典树构建的C++代码如下给出，供读者参考（代码说明中对一些内容作出了必要的解释，供读者选择性参考）：

字典树C++实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

struct AC_node {
    AC_node *parent;
    AC_node *son[26] = {nullptr};
    bool terminal = false;
    AC_node *fail = nullptr;
    char data;
    int depth;

    AC_node(char d, bool t, AC_node *p, int dep, AC_node *pt) {
        data = d;
        terminal = t;
        fail = p;
        depth = dep;
        parent = pt;
    }
};

class AC_Automaton {
private:
    AC_node *root;

public:
    AC_Automaton() {
        root = new AC_node('a', false, nullptr, 0, nullptr);
        // root->fail = root;
    }

    AC_node* getRoot() {
        return root;
    }

    bool addString(string& s) {
        AC_node *p = root;
        for(auto c: s) {
            if(p->son[c - 'a'] == nullptr) {
                p->son[c - 'a'] = new AC_node(c, false, nullptr, p->depth + 1, p);
            }
            p = p->son[c - 'a'];
        }// end for
        p->terminal = true;
        return true;
    }
};
字典树C++实现代码解释

上述代码中，AC_node类是节点的结构体：目前为止，仅需读者知道的成员变量意义如下：

变量名意义
AC_node *parent指向该节点的父节点的指针
AC_node *son[26]指向该节点子节点的指针
bool terminal终止标记
char data此节点存储的数据
int depth此节点位于的深度（根节点为0）

上述变量中的son指针数组的大小视字符集大小而变（在本例中，我们仅考虑26个英文小写字母，因此取值26），这样做的好处是我们可以在O(1)O(1)的时间内知道是否已经存在合适的子节点，若不存在则创建之，在字符集数量不大的情况下，这样做是值得的：我们仅付出了存储字符集个指针空间的代价，换取了高效的查询性能；teminal表示该节点是否属于一个终止节点：在构建字典树时，对每个模式的末尾字符所在的节点赋terminal = true表示该节点代表一个模式的终止。

其余变量的含义是显然的，在此不多赘述。

回溯问题

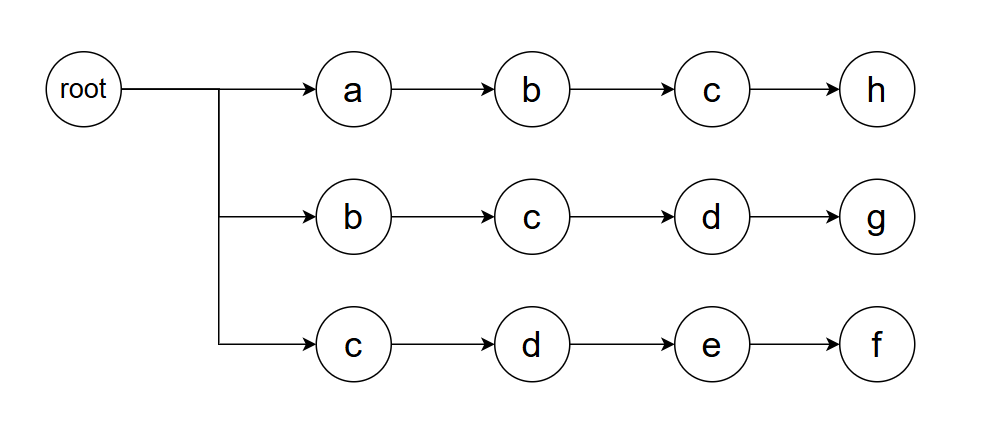
构建好了字典树，我们便要思考如何高效的对文本进行模式匹配。我们不妨思考一个简单的例子，在这个例子中：words = ["abcf", "bcdg", "cdef"]，s = "abcdef"。我们试图匹配这个字符串s，并找到其中出现的所有模式。首先，我们构建字典树如下。

构建字典树
构建字典树

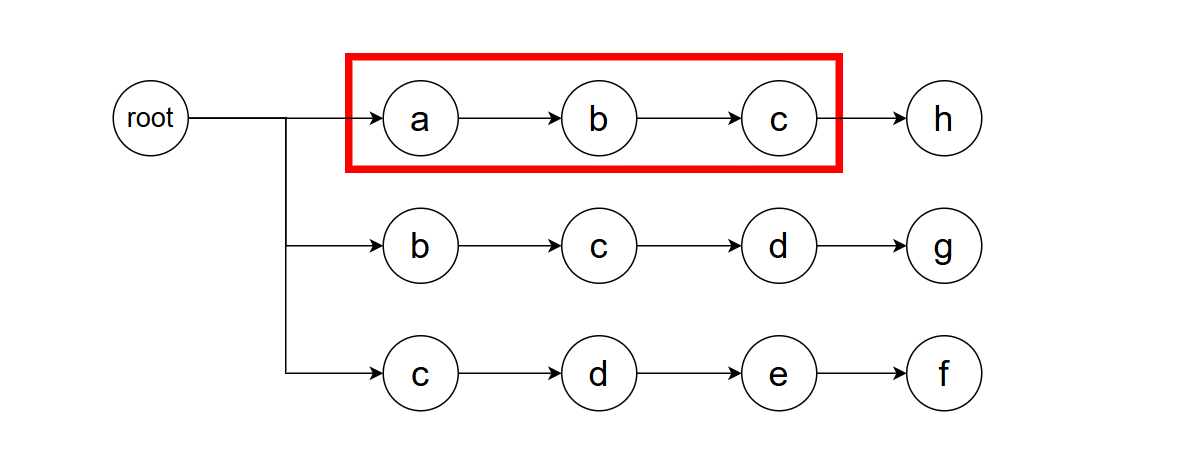
从字符串s开头进行匹配，我们可以一路匹配至abc（如红色矩形所示），因为这都满足第一个模式。

匹配过程
匹配过程

但是，当我们试图匹配d时遇到了麻烦：目前正在匹配的模式的下一个字符并非d而是f，显然不构成匹配。此时，我们需要设计一个回溯策略。怎么样的回溯策略是好的？一个方法是：我们需要将已构成匹配的字符串从头开始删减，直到能够构成新的匹配。

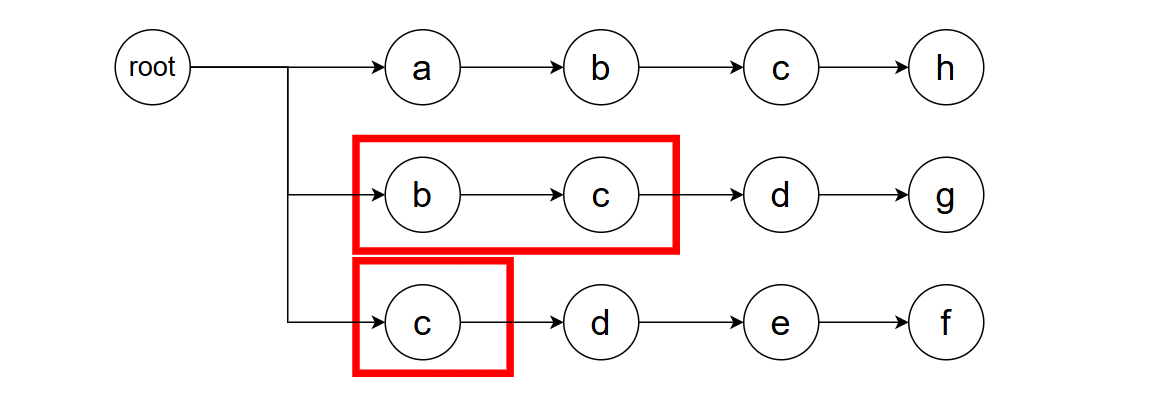
我们暂且不论如何做到这件事，仅在这个例子中，我们可以找到如下两种情况，使得这些匹配能够容纳新的字符d。

能够容纳新字符的匹配
能够容纳新字符的匹配

哪种选择是更好的？我们倾向于选择bcd这种匹配，因为它更长。想象一下，如果我们优先选择了短的，但后续出现了字符g，我们将永远错过bcdg这种模式（因为g无法匹配e，导致我们为找到新的可能匹配正试图缩减已匹配的字符串）；反过来的话，这个问题便不再存在了。

于是我们较为形式化地描述这一过程：我们记符号f(u,c)=vf(u,c)=v代表从节点uu匹配了字符cc从而转移到节点vv的过程，这个表示方法也成为 转移函数 。

当我们发现f(u,c)f(u,c)不存在（如上述例子中，从abc试图容纳d的方式不存在）时，我们试图缩短uu代表的字符串，使得其能够容纳字符cc（上述例子中，我们试图缩短abc来容纳字符d）。能够发现，我们寻找的便是uu代表的字符串的 最长后缀 （上述例子中，我们找到了abc的最长后缀bc）。我们记uu代表的字符串的最长后缀为fail(u)fail(u)。如果fail(u)fail(u)能够容纳字符cc，则f(fail(u),c)f(fail(u),c)就是我们转移到的新的匹配；否则，我们继续寻找fail(u)fail(u)的最长后缀，并尝试使它容纳cc。

上述步骤循环时，如果我们回溯到了根节点，但根节点也无法容纳cc（即没有以cc开头的模式存在，因为根节点实际上不匹配任何字符串），则该字符无法被匹配。我们跳过该字符，并从根节点开始匹配。

构建AC自动机

知道了上述过程，我们就可以构建AC自动机了。我们只需要在字典树上增加一些路径，使得无法构成匹配时，能够回溯到正确的位置。

假设我们需要设置v=f(u,c)v=f(u,c)的fail指针，即fail(v)fail(v)。也就是说，我们需要找到vv节点代表的字符串的最长后缀。由于fail(u)fail(u)是uu的最长后缀，如果f(fail(u),c)f(fail(u),c)存在，那么其一定是vv的最长后缀。否则，我们再试图找fail(u)fail(u)的最长后缀fail(fail(u))fail(fail(u))，判断f(fail(fail(u)),c)f(fail(fail(u)),c)是否存在…直到我们回溯到了根节点，且f(root,c)f(root,c)也不存在，那么cc无法匹配任何模式。

注意，由于上述实际上是一个递归过程，因此我们需要自行处理初始的fail指针。不过这也很容易，第一层的节点的fail指针全部指向root，因为对于单字符的字符串而言，其最长后缀就是空字符串（由root代表）。

下面是根据已有字典树构建fail指针的C++实现。

构建fail指针的C++实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

// struct AC_node {
//     ...
// };

class AC_Automaton {
private:
    AC_node *root;
    void childEnque(AC_node *p, queue<AC_node*> &q) {
        for(int i=0; i<26; i++) {
            if(p->son[i] != nullptr) {
                q.push(p->son[i]);
            }
        }
        return;
    }
public:
    // AC_Automaton() {
    //     ...
    // }

    // AC_node* getRoot() {
    //     return root;
    // }

    // bool addString(string& s) {
    //     ...
    // }

    void buildFail() {
        queue<AC_node*> q;
        // 深度为1的节点入队
        for(int i=0; i<26; ++i) {
            if(root->son[i]) {
                q.push(root->son[i]);
            }
        }
        while(!q.empty()) {
            // 队首出队
            AC_node *p = q.front();
            q.pop();

            // 分配失配指针
            // 特殊情况1： 深度为1的节点失配指针都是根节点
            if(p->depth == 1) {
                p->fail = root;
                // 将子节点入队
                childEnque(p, q);
                continue;
            }
            // 否则是普通情况
            AC_node* tmp = p->parent->fail;
            while(tmp) {
                if(tmp->son[p->data - 'a'] != nullptr) {
                    p->fail = tmp->son[p->data - 'a'];
                    break;
                }
                tmp = tmp->fail;
            }

            if(!tmp){//说明没找到合适的失配指针
                p->fail = root;
            }

            // 该节点所有子节点入队
            childEnque(p, q);

        }// end while
    }
};

匹配过程

完成了AC自动机的构建，我们进行多模块匹配的算法就极其简单了。我们使用一个指针存储目前已匹配的位置uu，即指向字典树中的某一个节点。对于下一个字符cc，如果f(u,c)f(u,c)存在，则直接将指针指向f(u,c)f(u,c)即可；反之，指向f(fail(u),c)f(fail(u),c)。

上述操作结束后，检查目前指向的节点的terminal，若为真，则已抵达某个模式字符串的末尾，即匹配成功；反之，继续读入文本的下一个字符，重复上述转移过程。

以下是匹配过程的C++实现。

进行匹配的C++实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

// struct AC_node {
//     ...
// };

class AC_Automaton {
private:
    AC_node *root;
    // void childEnque(AC_node *p, queue<AC_node*> &q) {
    //     ...
    // }
public:
    // AC_Automaton() {
    //     ...
    // }

    // AC_node* getRoot() {
    //     return root;
    // }

    // bool addString(string& s) {
    //     ...
    // }

    // void buildFail() {
    //     ...
    // }

    vector<vector<int>> searchPattern(string& s) {
        AC_node *p = root;
        vector<vector<int>> res;
        for(int i=0; i<s.length(); ++i) {
            char c = s[i];
            while(p != nullptr && p->son[c - 'a'] == nullptr) {
                p = p->fail;
            }
            if(p) {
                p = p->son[c - 'a'];    // 前进一步匹配
                // 判断是否匹配了完整的串
                if(p->terminal) {
                    res.push_back(vector<int>{i-p->depth + 1, i});
                }
            }else {
                p = root;
                continue;
            }
        }   // end for

        return res;
    }
};

AC自动机的完整模板代码

AC自动机的完整C++模板代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
struct AC_node {
    AC_node *parent;
    AC_node *son[26] = {nullptr};
    bool terminal = false;
    AC_node *fail = nullptr;
    char data;
    int depth;

    AC_node(char d, bool t, AC_node *p, int dep, AC_node *pt) {
        data = d;
        terminal = t;
        fail = p;
        depth = dep;
        parent = pt;
    }
};

class AC_Automaton {
private:
    AC_node *root;
    void childEnque(AC_node *p, queue<AC_node*> &q) {
        for(int i=0; i<26; i++) {
            if(p->son[i] != nullptr) {
                q.push(p->son[i]);
            }
        }
        return;
    }
public:
    AC_Automaton() {
        root = new AC_node('a', false, nullptr, 0, nullptr);
        // root->fail = root;
    }

    AC_node* getRoot() {
        return root;
    }

    bool addString(string& s) {
        AC_node *p = root;
        for(auto c: s) {
            if(p->son[c - 'a'] == nullptr) {
                p->son[c - 'a'] = new AC_node(c, false, nullptr, p->depth + 1, p);
            }
            p = p->son[c - 'a'];
        }// end for
        p->terminal = true;
        return true;
    }

    void buildFail() {
        queue<AC_node*> q;
        // 深度为1的节点入队
        for(int i=0; i<26; ++i) {
            if(root->son[i]) {
                q.push(root->son[i]);
            }
        }
        while(!q.empty()) {
            // 队首出队
            AC_node *p = q.front();
            q.pop();

            // 分配失配指针
            // 特殊情况1： 深度为1的节点失配指针都是根节点
            if(p->depth == 1) {
                p->fail = root;
                // 将子节点入队
                childEnque(p, q);
                continue;
            }
            // 否则是普通情况
            AC_node* tmp = p->parent->fail;
            while(tmp) {
                if(tmp->son[p->data - 'a'] != nullptr) {
                    p->fail = tmp->son[p->data - 'a'];
                    break;
                }
                tmp = tmp->fail;
            }

            if(!tmp){//说明没找到合适的失配指针
                p->fail = root;
            }

            // 该节点所有子节点入队
            childEnque(p, q);

        }// end while
    }

    vector<vector<int>> searchPattern(string& s) {
        AC_node *p = root;
        vector<vector<int>> res;
        for(int i=0; i<s.length(); ++i) {
            char c = s[i];
            while(p != nullptr && p->son[c - 'a'] == nullptr) {
                p = p->fail;
            }
            if(p) {
                p = p->son[c - 'a'];    // 前进一步匹配
                // 判断是否匹配了完整的串
                if(p->terminal) {
                    res.push_back(vector<int>{i-p->depth + 1, i});
                }
            }else {
                p = root;
                continue;
            }
        }   // end for

        return res;
    }
};
参考资料
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章

快来参与讨论吧~

- -