KMP算法

问题

  给定一个字符串$A$，要求从字符串$A$中查找另一个字符串$B$是否出现。如果出现，返回查找的字符串$B$在$A$中的位置，否则返回-1。

最简单的解决方法——枚举法

  枚举法当然可以解决这个问题：我们可以在从$A$字符串中取第一位，然后逐位往后与$B$串比较。如果匹配则返回答案；若不匹配，则从$A$字符串的第二位开始，重复上述操作，直到找到字符串位置或者字符串$A$被遍历完毕。

  我们来分析一下这个的算法复杂度。我们假设字符串$A$和$B$的长度分别为$m$和$n$，那么这个算法的最差情况需要比较$m\times n$次，即这个算法是$O(m\times n)$的。

KMP算法

  KMP算法是一个很好的解决算法，它可以 最多只扫描一次字符串$A$ 就能完成任务，即它的算法复杂度是$O(n)$的。之所以被叫作KMP算法，是因为它是由Knuth、Morris、Pratt三个人提出的。下面来介绍一下该算法的思想。

简单的直观模拟

  为了说明KMP的大致过程，我们先给出一个例子。

一个例子

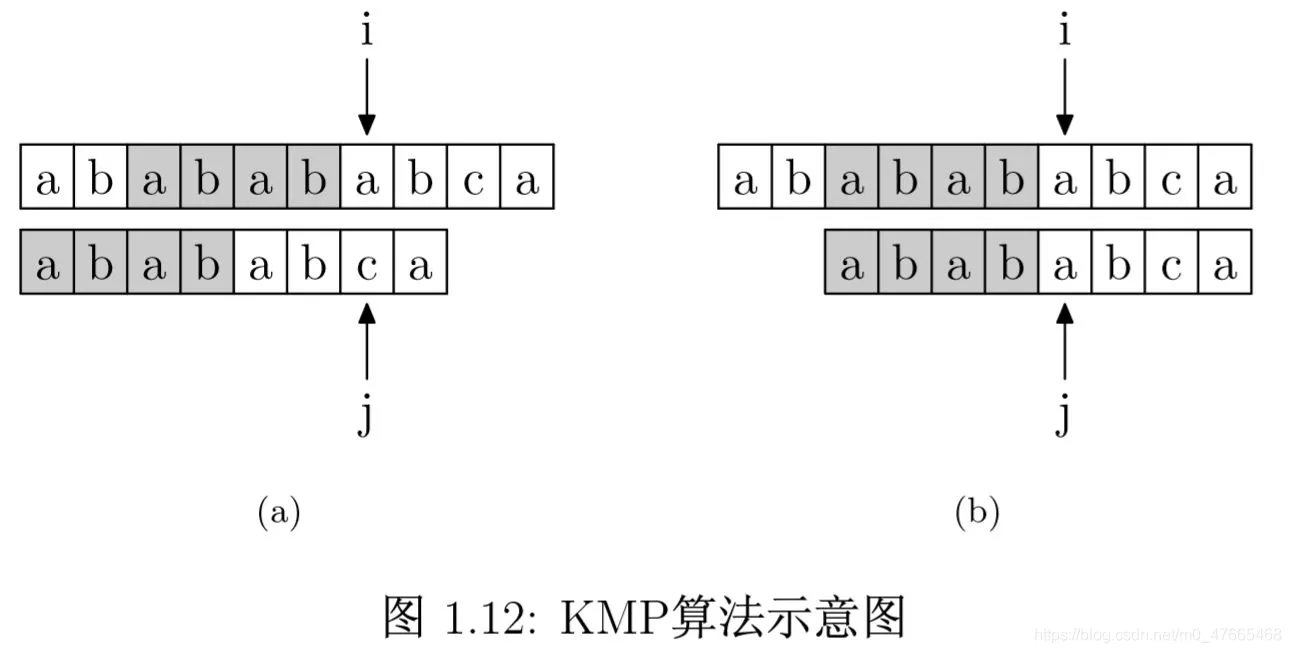
  我们参考上例，并且称大数组为$ch$，目标数组为$target$。我们从第一位开始逐个比较$ch$和$target$中的每一位，直到不匹配为止，如图(a)所示。我们发现，$ch[6]!=target[6]$。但是在$i\leqslant 5$都有$ch[i]=target[i]$。我们此时不将$target$往后移动一位，选择往后移动两位，因为**这个时候$ch[2]$到$ch[6]$仍然和目标字符串是匹配的。**我们可以证明，这个位置是除了初始位置外第二个可能的匹配发生的位置。因为如果在此之前还存在一个匹配的字符串，那么我们要么已经找到了它，要么重定位会定位到它，而不是 $ch[2]$ 。如果你能理解这点，这就是KMP算法的基本原理。

失效函数

失效函数原理

  那么随之而来的问题是：我们如何确定应该向后移动几位呢？ 以及，如果每次向后移动都可以看做字符串$target$正在比较元素的后退，（正如上例中本在比较$target[6]$和$ch[6]$，向后移动后相当于比较$target[4]$和$ch[6]$） 那么到底后退几位呢？ 如果我们把字符串中正在比较的元素位置记作$j$，后退后正在比较$j^\prime$，那么我们可以知道它们满足：$target[0]$到$target[j^\prime]$之间的字符串和$target[j-j^\prime]$到$target[j]$之间的字符串完全相同。这里需要读者仔细理解一下，我们实际上取的$j^\prime$是使得$target$中前$j^\prime+1$和后$j^\prime+1$个字符完全相同，也就是我们在前一节说的直观模拟的结果。

  我们把$j$和$j^\prime$的对应关系称为失效函数，即

$$j^\prime =P[j].$$

有了这个对应关系，我们就可以轻松决定，当字符串正在比较位置$i,j$相同，即$ch[i]=target[j]$时，但位置$i+1,j+1$不同，即$ch[i+1]\neq target[j+1]$时，$j$需要更新成什么了。

失效函数的算法

  我们从上述论断中可以知道，失效函数的产生只和目标数组$target$有关，因此我们可以对目标数组预处理，得到其失效函数。那么，失效函数的算法是什么呢？

  首先，我们知道对于$target[0]$，是没有满足失效函数定义的下标$j^\prime$的，那么，我们定义这种条件下，其失效函数值为-1。然后我们用递推的方式求出其他元素的失效函数。我们现在要求下标为$j$的元素的失效函数，那么我们考察$j-1$位置上的元素，其失效函数的值为$j_0$，那么也就是说，$target[0]$到$target[j_0]$之间的字符串和$target[j-1-j_0]$到$target[j-1]$之间的字符串完全相同，那么我们只要比较$target[j_0+1]$和$target[j]$是否相同，即比较$target[P[j-1]+1]$和$target[j]$是否相同。如果也相同，那么$P[j-1]+1=P[j]$；否则，我们可以令$P[j_0]$是新的$j_0$，继续反复上次的比较，直到找到$target[0]$并且$target[0]$和$target[j]$也不相等，那么其失效函数的值为-1 。

失效函数的实现

  这节给出失效函数failurefunc()的实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

int* failurefunc(const seqString& target)const{
    int* p=new int[target.len];//申请一个数组，存放失效函数
    int j;

    p[0]=-1;//首元素的失效函数值为-1
    for(int i=1;i<target.len;++i){
        j=i-1;//往前退一位

        while(j>=0&&target.data[p[j]+1]!=target.data[i]) j=p[j];//如果最长相同子序列不存在，那么缩短相同子序列长度
        if(j<0) p[i]=-1;//直到找完都没有找到，则失效函数为-1
        else p[i]=p[j]+1;//找到了，更新失效函数的值
    }//end for

    return p;
}//end function

查找函数

  有了上面的失效函数，我们可以完成KMP算法中的查找部分了。

查找函数的原理

  查找函数使用两个指针$i$和$j$，分别指向字符串$ch$和$target$中正在比较的元素。从两字符串头开始，对$i,j$一同自增，直到发现$ch[i]!=target[j]$就停止；此时，利用失效函数，对$j$的值进行更新，更新为其前一个元素失效函数的值后的元素，即$P[j-1]+1$，然后重新比较$i$和$j$，重复上述步骤，直到$j=0$时还是无法匹配，则固定$j$，对$i$自增，直到匹配为止。搜索过程退出的条件是：找到了$target$的位置，即$j=target.len-1$；或者未找到，即$i=ch.len-1$。

查找函数的实现

  本节实现查找函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

int find(const seqString & ch, const seqString & target){
    int* p=NULL;//存放失效函数
    p=failurefunc(target);//获取失效函数

    int i=j=0;//定位指针

    while(i<ch.len&&j<target.len){
        if(ch.data[i]==target.data[j]) {i++;j++;}//相等则自增
        else if(j==0) i++;//不相等但是j已经为零时，i自增
            else j=p[j-1]+1;//否则更新j的值 
    }//end while

    delete p;//释放内存

    if(j==target.len) //比较完最后一个字符后，j又自增了一次，所以应该是最后一个元素的下标+1
        return i-j;//如果找到了以后才退出，那么返回位置
    else
        return -1;//否则就是没找到，返回未找到
}

后记

  KMP算法的时间复杂度是$O(n)$的，因为我们即便可能需要扫描目标字符串许多遍，但主字符串我们只需要扫描一遍，也就是说不会超过$n$次。KMP算法为什么能节省时间，本质上使我们利用了扫描匹配过程中匹配失败的信息。对于匹配失败的节点，我们利用两个指针直接跳过了许多次扫描，因而节省了时间。可以说，KMP算法相比于枚举法有着更高的信息利用率。

许可协议

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。

分享文章