强化学习是指导智能体如何根据环境反馈而选择最佳决策的学习方式，本文主要介绍强化学习的基本概念和优化目标。

强化学习基本概念

什么是强化学习？

Reinforcement learning is learning what to do—how to map situations to actions——so as to maximize a numerical reward signal. ----- Richard S. Sutton and Andrew G. Barto 《Reinforcement Learning: An Introduction II》

强化学习(Reinforcement learning，RL)讨论的问题是一个智能体(agent)怎么在一个复杂不确定的环境(environment)里面去极大化它能获得的奖励。通过感知所处环境的状态(state)对动作(action)的反应(reward)，来指导更好的动作，从而获得最大的收益(return)，这被称为在交互中学习，这样的学习方法就被称作强化学习。

强化学习的基本流程和概念

在强化学习中，存在一些基本的概念。理解清楚这些概念对我们后续的学习具有重要的铺垫意义，本部分总结阅读本文需要了解的基础概念，并给出符号表示。

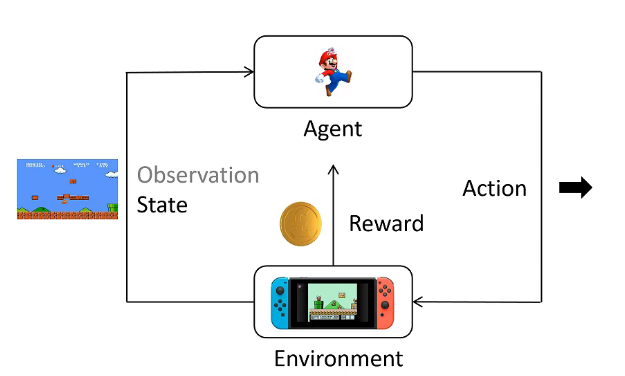
一般来说，强化学习的流程如下图所示：

强化学习的基本流程

Agent基于对环境的观察（又称state）选择下一步行动action，同时，Agent产生的行动action又会反作用于环境（Environment），从而推进到下一个State。上述过程循环往复，形成Agent和Environment的基本交互流程。

为了形式化地描述上述过程，对其中的一些概念进行定义。

• 动作空间：是Agent每个状态下可选择的动作的集合，一般使用如集合 $\{a_1, a_2, \dots, a_n\}$ 的形式表示；
• 策略函数(Policy)：表示在给定状态下，Agent采取不同行动的概率值，是一个概率分布。通常以 $P(a_i \mid s_t)$ 的形式表示；
• 轨迹(Trajectory)：Agent所处的状态以及采取的行动的序列，一般为 $\{s_0, a_0, s_1, a_1, \dots, s_m, a_m\}$；
• 奖励(Reward)：表示Agent每一次行动后环境给出的评价；
• 回报(Return)：表示从当前时刻起，直到结束时间所获得的总的奖励之和。依据算法不同，可能会引入衰减因子 $\gamma$ 。

强化学习的优化目标

目标函数

强化学习的优化目标，就是要找出一条轨迹，使得其能够带来最大的总回报。也就是说，我们需要选出一条轨迹 $\tau$ ，使得：

$$E(R(\tau))_{\tau \sim P_\theta (\tau)}=\sum _{\tau}R(\tau)P_\theta (\tau)$$

最大化。其中， $\theta$ 是模型参数。我们训练模型，就是找到一组更好的参数 $\theta$。

梯度上升法

要最大化上述目标函数，通常使用的方法是梯度上升法，也即求取上述目标函数的梯度值，而后依据学习率(Learning Rate)，进行梯度上升。上述目标函数的梯度可由如下运算获得：

$$\begin{aligned} \nabla E(R(\tau))_{\tau \sim P_\theta (\tau)}&=\sum _{\tau}R(\tau)\nabla P_\theta (\tau)\\ &=\sum _{\tau}P_\theta (\tau)R(\tau)\dfrac{\nabla P_\theta (\tau)}{P_\theta (\tau)}\\ &\approx \dfrac{1}{N}\sum _{i=1}^N R(\tau^i)\dfrac{\nabla P_\theta (\tau ^i)}{P_\theta (\tau ^i)}\\ &= \dfrac{1}{N}\sum _{i=1}^N R(\tau^i)\nabla \log P_\theta (\tau ^i). \end{aligned}$$

上述的不等号由大数定律而得，即使用多次随机采样的结果来逼近期望值。$\tau ^i$ 的上标 $i$ 表示采样次数，对于不同的两次采样，均独立且服从于 $P _\theta (\tau)$ 的分布。

对于轨迹 $\tau ^i$ 的概率分布 $P(\tau ^i)$，可以使用条件概率将其拆分开，如下表示：

$$P_\theta (\tau ^i) = \prod _{t=1}^{T_i} P _\theta (a^i_t \mid s^i_t).$$

因此，上述梯度还可以进一步表示为：

$$\begin{aligned} \nabla E(R(\tau))_{\tau \sim P_\theta (\tau)}&=\dfrac{1}{N}\sum _{i=1}^N R(\tau^i)\nabla \log P_\theta (\tau ^i)\\ &=\dfrac{1}{N}\sum _{i=1}^N R(\tau^i)\nabla \log \prod _{t=1}^{T_i} P _\theta (a^i_t \mid s^i_t)\\ &=\dfrac{1}{N}\sum _{t=1}^{T_i}\sum _{i=1}^N R(\tau^i)\nabla \log P _\theta (a^i_t \mid s^i_t). \end{aligned}$$

上述优化目标对应的 损失函数(Loss Function) 为：

$$\text{loss} =-\dfrac{1}{N}\sum _{t=1}^{T_i}\sum _{i=1}^N R(\tau^i) \log P _\theta (a^i_t \mid s^i_t).$$

在一次训练中，通过与环境进行多次完整的互动，得到每次轨迹的总回报值 $R(\tau ^i)$ ，并记录在每一个不同状态下的行动概率分布 $P_\theta (a^i_t \mid s^i_t)$ ，进行反向传播，降低loss。

上述loss函数存在的问题

上述loss函数尽管已经能体现出不错的训练效果，但其还存在一些细节上的问题。比如：

1. 对于某条给定的轨迹 $\tau ^i$ ，其中每一步行动的价值都等同于整个轨迹的回报 $R(\tau ^i)$ 吗？
2. 若某条轨迹 $\tau ^i$ 的回报小于零，那么这条轨迹中所有的行动选择都是错误的吗？

先看第一个问题。显然，根据因果关系，在某一时刻的行动抉择，理应只能够影响后续的回报，而对前面的回报无法产生影响。因此，回报 $R(\tau ^i)$ 应该使用 $R_t^i$ 来替代：

$$R_t^i = \sum_{t^\prime = t}^{T_i} \gamma ^{t^\prime - t}r_{t^\prime} ^i.$$

上述中的衰减因子 $\gamma$ 是一个超参数，它表示如果奖励一致，那么更早地获取奖励比更晚要好，这也符合一般直觉。

第二个问题中，我们假定这样一个场景。在某个状态下，动作空间为 $\{A,B,C\}$，且三者对应的回报为 $2,5,4$。显然，三者都大于零，但是三种动作都是值得奖励的吗？反过来，如果三者对应的回报为 $-4,-1,-7$，那么三者都是值得惩罚的吗？事实上并不是。我们需要引导Agent做出当下的最优解，而不仅仅局限于回报的绝对大小。因此，在状态 $s_t^i$ 下，我们引入Baseline $B(s_t^i)$ ，用来衡量该状态下各种不同行动的 平均回报 ，并以此作为基准鼓励Agent采取能够获得高于平均回报的动作。

结合上述两个分析，最优化目标的梯度被更新为：

$$\dfrac{1}{N}\sum _{t=1}^{T_i}\sum _{i=1}^N (R_t^i-B(s_t^i))\nabla \log P _\theta (a^i_t \mid s^i_t).$$

行动价值、状态价值和优势

引出了上述公式后，我们不妨再形式化一些概念，好让上述推导变得更加清晰明显。

行动价值函数(Action Value Function)，顾名思义，表示在某一状态下采取给定行动所能带来的回报。该函数用以取代上面的 $R^i_t$ ，原因是因为该值为随机采样得到的结果，具有较大的不确定性。行动价值函数 $Q_\theta (s_t,a)$ 则能较为稳定地反应状态 $s_t$ 下选择行动 $a$ 所得的回报。

状态价值函数(State Value Function), 用于评估状态的好坏，也可以理解成该状态下选择不同行动的平均回报，用 $V_\theta (s_t)$ 表示。

优势函数(Advantage Function)，用于描述在当前状态下采取某一行动的优势的度量。其与上述函数存在关系：

$$A_\theta (s_t, a)=Q_\theta (s_t, a)-V_\theta (s_t).$$

经过更严格的定义，优化目标可以继续被改写为：

$$\dfrac{1}{N}\sum _{t=1}^{T_i}\sum _{i=1}^N A_\theta (s_t^i, a^i)\nabla \log P _\theta (a^i_t \mid s^i_t).$$

行动价值、状态价值和优势的计算方式

关于上述三个函数，一个比较显然的关系式为：

$$Q_\theta (s_t, a) = r_t + \gamma V_\theta (s_{t+1}).$$

这表示：在当前状态采取某一行动所获得的回报应该等于当前瞬间环境给出的奖励，以及转移到的新状态所蕴含的回报的折扣之和。

严格来说，上式应通过如下方法导出：

$$\begin{aligned} Q_\theta (s_t, a)&=E(r_t+\gamma r_{t+1} + \dots \mid s_t, a_t)\\ &=E(r_t\mid s_t, a_t)+\gamma E(r_{t+1} + \gamma r_{t+2} + \dots\mid s_t,a_t)\\ &=E(r_t\mid s_t, a_t) + \gamma \sum_{s_{t+1}}P_\theta(s_{t+1})V_\theta(s_{t+1}). \end{aligned}$$

于是，一步采样（表示为 $A$ 的上标）得到的优势函数可以展开为如下形式：

$$A_\theta^1 (s_t, a) = r_t + \gamma V_\theta (s_{t+1}) - V_\theta (s_t).$$

另一较不显然的公式为：

$$V_\theta(s_t)\approx r_t+\gamma V_\theta(s_{t+1}).$$

严格来说，上式应通过如下方法导出：

$$\begin{aligned} V_\theta(s_t)&=E(r_t+\gamma r_{t+1}+\dots \mid s_t)\\ &=E(r_t\mid s_t) +\gamma E(r_{t+1} + \gamma r_{t+2}\mid s_t)\\ &=E(r_t\mid s_t) + \gamma \sum_{s_{t+1}}P_\theta(s_{t+1})V_\theta(s_{t+1})\\ &\approx r_t + \gamma V_\theta(s_{t+1}). \end{aligned}$$

因此，可以通过展开 $V_\theta (s_{t+i})$ 来获取多步采样的优势函数 $A_\theta (s_t,a)$.例如两步采样：

$$A_\theta ^2=r_t+\gamma r_{t+1} + \gamma ^2V_\theta(s_{t+2})-V_\theta (s_t),$$

三步采样：

$$A_\theta^3=r_t+\gamma r_{t+1} + \gamma ^2r_{t+2} + \gamma ^3 V_\theta(s_{t+3}) - V_\theta(s_t),$$

等等。

为了表示方便，使用新的记号 $\delta _t^V$ 表示在状态 $V$ 下，$t$ 时刻做出选择后产生的优势：

$$\delta _t^V = r_t + \gamma V_\theta(s_{t+1}) - V_\theta (s_t).$$

那么 $k$ 步优势可以简化成：

$$A_\theta ^k=\sum_{i=0}^{k-1}\gamma ^i \delta^V_{t+i}.$$

广义优势估计

广义优势估计(Generalized Advantage Estimation, GAE) 是一种综合考虑了多步优势的一种优势估计方法，并使用一定的权重来平衡之。

$$\begin{aligned} A_\theta ^{GAE} &= (1-\lambda)(A_\theta ^1 + \lambda A_\theta ^2 + \lambda ^2A_\theta ^3 + \dots)\\ &=\sum_{b=0}^\infty (\gamma \lambda)^b\delta_{t+b}^V. \end{aligned}$$

总结

通过上述大量的数学推导，我们得到的了最后的优化目标：

$$\dfrac{1}{N}\sum _{t=1}^{T_i}\sum _{i=1}^N A_\theta ^{GAE}\nabla \log P _\theta (a^i_t \mid s^i_t).$$

其中，广义优势估计的计算方法为：

$$A_\theta ^{GAE} = \sum_{b=0}^\infty (\gamma \lambda)^b\delta_{t+b}^V,$$

其中，$\delta _t^V = r_t + \gamma V_\theta(s_{t+1}) - V_\theta (s_t)$.

在训练过程中，需要另一个模型来拟合状态价值函数 $V_\theta(s_t)$，其拟合目标为：

$$V_\theta(s_t) = \sum_{t^\prime = t}^{T_i} \gamma ^{t^\prime - t}r_{t^\prime} ^i.$$

因此，完成上述过程的训练一共需要三个模型：策略模型(Policy Model)、奖励模型(Reward Model)和回报模型(Reward Model)。